Cách vẽ đồ thị hàm số bậc hai (trên giấy và trên máy tính) |
- Cách vẽ đồ thị hàm số bậc hai (trên giấy và trên máy tính)
- 2 cách tính khoảng cách từ một điểm đến một đường thẳng
- Cách tính diện tích và thể tích của hình nón, hình nón cụt
| Cách vẽ đồ thị hàm số bậc hai (trên giấy và trên máy tính) Posted: 18 Apr 2022 06:40 AM PDT Hàm số bậc hai có dạng đầy đủ là $y=ax^2+bx+c$ với điều kiện $a \neq 0$. Tuy nhiên, do giới hạn của chương trình Toán học Trung học cơ sở chưa học khái niệm Đạo hàm và việc vẽ đồ thị hàm số bậc hai ở dạng đầy đủ chỉ bằng các kiến thức của Đại số sơ cấp khá là phức tạp. Vậy nên, thay vì hướng dẫn vẽ đồ thị của hàm số bậc hai ở dạng đầy đủ thì mình sẽ hướng dẫn cho các bạn cách vẽ với dạng thiếu là $y=ax^2$. Mục Lục Nội Dung I. Sơ lược về đồ thị của hàm số bậc haiĐồ thị của hàm số bậc hai $y=ax^2$ là một đường cong đi qua gốc tọa độ $O=(0; 0)$ và nhận trục tung $Oy$ làm trục đối xứng. Vì đường cong này là một dạng đường cong thường gặp trong Toán học cũng như trong cuộc sống nên nó đã được đặt một tên riêng, gọi là Parabol.
II. Cách vẽ đồ thị của hàm số bậc 2 trên giấyNếu được, ngoài bút chì và thước thẳng ra thì bạn hãy chuẩn bị thêm thước Parabol để việc vẽ đồ thị được chính xác và nhanh chóng hơn nhé.
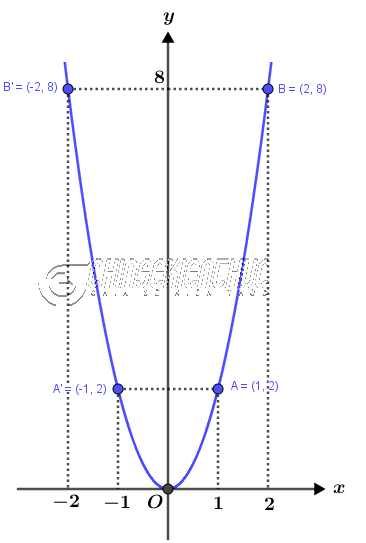
Đồ thị hàm số $y=ax^2$ luôn đi qua gốc tọa độ $O=(0; 0)$ và nhận trục tung $Oy$ làm trục đối xứng nên ta chỉ cần tìm 2 điểm ở bên phải hoặc ở bên trái trục tung $Oy$ rồi lấy thêm 2 điểm đối xứng Bạn có thể lấy nhiều hơn 2 điểm hoặc lấy hai điểm theo cách khác nhưng mình thường lấy $A=(1; a)$ và $B=(2; 4a)$ => sau đó lấy đối xứng qua trục tung $Oy$ ta được $A'=(-1; a)$ và $B'=(-2; 4a)$ Cuối cùng bạn dùng thước Parabol để vẽ đường cong đi qua 5 điểm $A, B ,A', B'$ và $O$ là xong. Ví dụ 1: Vẽ đồ thị của hàm số bậc hai $y=2x^2$ Dễ thấy điểm $A=(1; 2)$ và $B=(2; 8)$ thuộc đồ thị hàm số. Lấy đối xứng qua trục tung $Oy$ ta được $A'=(-1; 2)$ và $B'=(-2; 8)$ cũng thuộc đồ thị hàm số. Gốc tọa độ $O=(0; 0)$ dĩ nhiên thuộc đồ thị hàm số => Như vậy chúng ta đã có 5 điểm thuộc đồ thị hàm số là $A=(1; 2), B=(2; 8), A'=(-1; 2), B'=(-2; 8)$ và $O=(0; 0)$
Nhận xét về đồ thị: Vẽ đồ thị hàm số là một trong những cách dễ nhất để minh họa các tính chất của hàm số. Cụ thể trong trường hợp này là …
Một số lưu ý khi vẽ:
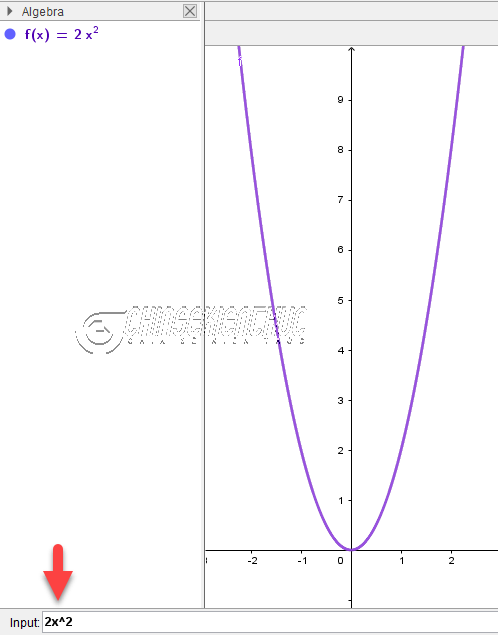
III. Cách vẽ đồ thị của hàm số bậc hai trên máy tính#1. Đối với phần mềm GeoGebraCách vẽ bằng phần mềm GeoGebra rất đơn giản, bạn chỉ cần nhập
#2. Đối với ứng dụng CaculatorBước 1. Nhấn tổ hợp phím
Bước 2. Chọn biểu tượng
Bước 3. Chọn vào biểu tượng
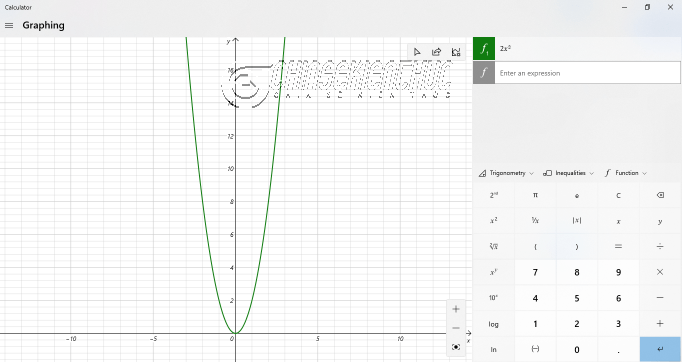
Bước 4. Nhập
Để xuất đồ thị ra thì bạn hãy nhấn chuột phải vào lưới tọa độ => chọn Bạn cũng nên định dạng lại đồ thị cho phù hợp với yêu cầu của công việc trước khi xuất ra bạn nhé. IV. Lời kếtNhư vậy là mình đã hướng dẫn xong cho bạn cách vẽ đồ thị hàm số bậc 2 rồi nhé. Cũng rất đơn giản phải không nào ! Trước khi tạm ngừng bút thì mình xin có một gợi ý nhỏ nữa muốn gửi đến các bạn. Thay vì trình bày như trong bài viết thì bạn có thể trình bày tọa độ 5 điểm dưới dạng bảng (ở trường vẫn hay áp dụng). Mặc dù trình bày theo cách này tuy không chuyên nghiệp nhưng nó Sư phạm, dễ tiếp cận với các bạn mới làm quen, các bạn hay bị sai sót khi tính toán. Okay. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ! CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé ! |
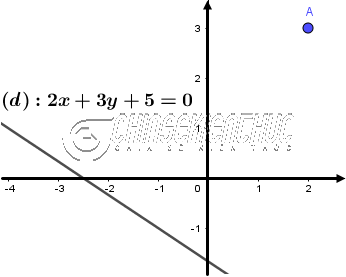
| 2 cách tính khoảng cách từ một điểm đến một đường thẳng Posted: 18 Apr 2022 02:20 AM PDT Nếu như việc tính khoảng cách từ một điểm đến một đường thẳng nằm trên mặt phẳng không có gì khó khăn thì việc tính khoảng cách từ một điểm đến một đường thẳng nằm trong không gian lại khá là phức tạp. Thông thường bạn sẽ cần thực hiện các bước sau: Viết phương trình đường thẳng đi qua điểm đã cho và vuông góc với đường thẳng đã cho, tiếp theo tìm giao điểm của đường thẳng vừa viết và đường thẳng đã cho, và cuối cùng là tính khoảng cách giữa giao điểm vừa tìm được với điểm đã cho. Các bước trên dù không quá phức tạp nhưng nó cũng tốn khá nhiều thời gian và công sức, đặc biệt vì tính toán khá nhiều nên dễ xảy ra sai sót. Vậy nên hôm nay, mình sẽ hướng dẫn các bạn cách tính khoảng cách từ một điểm đến một đường thẳng trong không gian bằng một cách khác dễ dàng hơn khá nhiều. Cách này chủ yếu dựa vào tích có hướng hoặc máy tính CASIO fx-580VN X. Đọc thêm: Mục Lục Nội Dung I. Trường hợp: Điểm và đường thẳng nằm trên mặt phẳng#1. Công thức tính khoảng cách từ một điểm đến một đường thẳngTính khoảng cách từ điểm $M_1$ và đường thẳng $(d)$ biết $M_1=(x_1; y_1)$ và đường thẳng $(d): Ax+By+C=0$ $(M_1; (d))=\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}$ #2. Ví dụ minh họaTính khoảng cách từ điểm $A=(2; 3)$ đến đường thẳng $(d): 2x+3y+5=0$[/toggle]
Lời Giải: Áp dụng công thức $\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}$ ta được $\frac{|2.2+3.3+5|}{\sqrt{2^2+3^2}}=\frac{18\sqrt{13}}{13} \approx 5$ => Vậy khoảng cách từ điểm $A=(2; 3)$ đến đường thẳng $(d): 2x+3y+5=0$ gần bằng 5 ĐVĐD II. Trường hợp: Điểm và đường thẳng nằm trong không gian#1. Cách tính khoảng cách từ một điểm đến một đường thẳngTính khoảng cách từ điểm $M_1=(x_1; y_1; z_1)$ đến đường thẳng $(d): \frac{x-x_0}{p}=\frac{y-y_0}{q}=\frac{z-z_0}{r}$ $\frac{\sqrt{[(y_{1}-y_{0}).r-q.(z_{1}-z_{0})]^{2}+[(z_{1}-z_{0}).p-r(x_{1}-x_{0})]^{2}+[(x_{1}-x_{0}).q-p(y_{1}-y_{0})]^{2}}}{\sqrt{p^2+q^2+r^2}}$
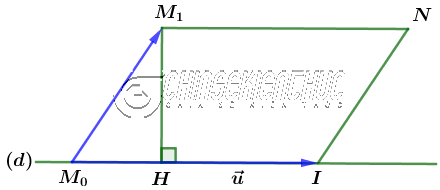
#2. Cách chứng minhDễ thấy đường thẳng $(d)$ đi qua điểm $M_0=(x_0; y_0; z_0)$ và có véc-tơ chỉ phương $\vec{u}=(p; q; r)$ $\overrightarrow{M_0M_1}$ và $\vec{u}= \overrightarrow{M_0I}$ tạo thành một hình bình hành có diện tích S
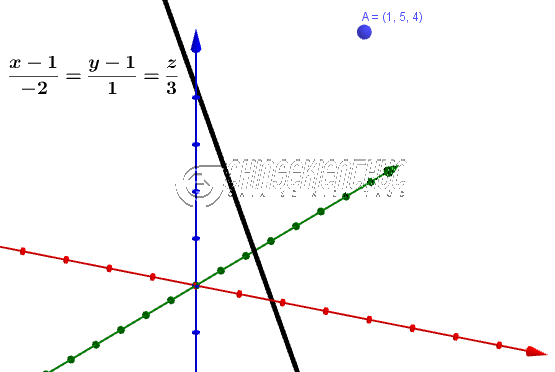
$h=M_1H=\frac{S}{|\overrightarrow{M_0I}|}=\frac{|[\overrightarrow{M_0M_1}; \vec{u}]|}{|\vec{u}|}$ #3. Ví dụ minh họaTính khoảng cách từ điểm $A=(1; 5; 4)$ đến đường thẳng $(d):\frac{x-1}{-2}=\frac{y-1}{1}=\frac{z}{3}$
Lời Giải: Dễ thấy đường thẳng $(d)$ đi qua điểm $M_0=(1; 1; 0)$ và có véc-tơ chỉ phương $\vec{u}=(-2; 1; 3)$ Suy ra $\overrightarrow{M_0A}=(0; 4; 4)$ Tích có hướng của $\overrightarrow{M_0A}$ và $\vec{u}$ bằng $(8; -8; 8)$ Độ dài tích có hướng của $\overrightarrow{M_0A}$ và $\vec{u}$ bằng $\sqrt{(8)^2+(-8)^2+(8)^2}=8\sqrt{3}$ Độ dài $\vec{u}$ bằng $\sqrt{(-2)^2+(1)^2+(3)^2}=\sqrt{14}$ => Vậy khoảng cách từ điểm $A$ đến đường thẳng $(d)$ là $\frac{8\sqrt{3}}{\sqrt{14}}= \frac{4\sqrt{42}}{7}\approx 3.7$ #4. Cách tính khoảng cách từ một điểm đến một đường thẳng bằng CASIO fx-580VN XBước 1. Chọn phương thức tính toán Vector
Bước 2. Lần lượt gán $\overrightarrow{M_0A}, \vec{u}$ cho VctA, VctB
Bước 3. Tích tích có hướng của $\overrightarrow{M_0A}$ và $\vec{u}$
Bước 4. Tính khoảng cách theo công thức (Abs(VctAns))⨼(Abs(VctB))
Chú ý ⨼ là phím phân số III. Lời kếtCông thức tính khoảng cách từ một điểm đến một đường thẳng nằm trong không gian (ý mình là tính trực tiếp ý) tuy là có, nhưng quá phức tạp và rất khó nhớ. Bạn chỉ có thể nhớ được khi bạn có trí nhớ rất rất tốt. Vậy nên thay vì cố gắng nhớ một cách máy móc bạn hãy xem phần #2 trong mục II (cách chứng minh) để biết cách mà mình đã dùng để xây dựng công thức, từ đó việc ghi nhớ công thức cũng dễ dàng hơn. Trong quá trình áp dụng nếu là …
Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ! Đọc thêm: CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé ! |
| Cách tính diện tích và thể tích của hình nón, hình nón cụt Posted: 18 Apr 2022 01:57 AM PDT Tương tự như hình cầu, hình nón và hình nón cụt cũng là những khối tròn xoay thường gặp trong Toán học cũng như trong thực tiễn.
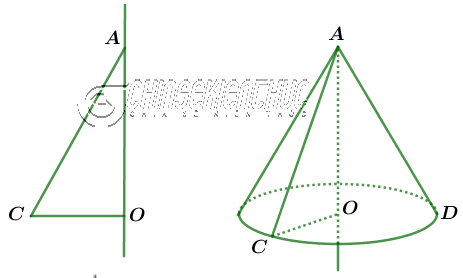
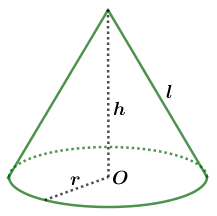
Vâng! Nón lá, kem ốc quế, cái quặng, cái xô, đèn ngủ, chậu kiểng, … là những hình ảnh thường gặp nhất và dễ liên tưởng nhất đến hình nón. Nhằm giúp các bạn có cái nhìn chi tiết hơn về hình nón và hình nón cụt, cũng như để các bạn biết cách tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón/ hình nón cụt nên mình đã soạn biên rất chi tiết bài viết này. Ok. Ngay bây giờ chúng ta hãy cùng nhau tìm hiểu nhé … Mục Lục Nội Dung I. Hình nón#1. Hình nón là gì?Định nghĩa: Hình nón là hình được tạo ra khi quay tam giác vuông một vòng quanh một cạnh góc vuông cố định.
Khi quay tam giác vuông AOC (vuông ở O) một vòng quanh cạnh góc vuông AO cố định chúng ta sẽ được một hình nón
Sau khi quay cạnh …
#2. Tính chất của hình nón
#3. Cách tính diện tích xung quanh của hình nónDiện tích xung quanh của hình nón sẽ bằng tích của $\pi$, độ dài bán kính, độ dài đường sinh Công thức: $S_{xq}=\pi.r.l$ Chú ý: Độ dài của đường sinh sẽ bằng căn bậc hai của tổng bình phương độ dài bán kính và chiều cao. #4. Cách tính diện tích toàn phần của hình nónDiện tích toàn phần của hình nón sẽ bằng tổng của diện tích xung quanh, diện tích đáy Công thức: $S_{tp}=S_{xq}+\pi.r^2=\pi.r.l+\pi.r^2$
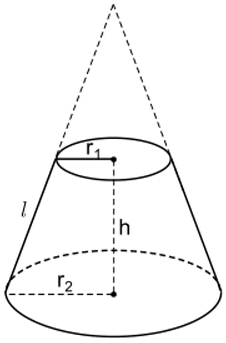
#4. Cách tính thể tích của hình nónThể tích của hình nón sẽ bằng tích của một phần ba, $\pi$, bình phương độ dài bán kính, chiều cao Công thức: $V=\frac{1}{3}.\pi.r^2.h$ Ví dụ 1: Cho hình nón có độ dài bán kính bằng $r=6~cm$ và chiều cao bằng $h=8~cm$ Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình chóp Lời Giải: Công việc đầu tiên cần làm là tính độ dài của đường sinh l của hình nón Độ dài đường sinh l của hình nón đã cho sẽ được tính theo công thức $\sqrt{r^2+h^2}=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10~cm$ $S_{xq}=\pi.r.l=\pi.6.10=60\pi \approx 188.5~cm^2$ $S_{tp}=S_{xq}+\pi.r^2=60\pi+\pi.6^2=60.\pi+36.\pi=96.\pi \approx 301.6~cm^2$ $V=\frac{1}{3}.\pi.r^2.h=\frac{1}{3}.\pi.6^2.8=96.\pi \approx 301.6~cm^3$ Vậy diện tích xung quanh, diện tích toàn phần và thể tích của hình chóp đã cho lần lượt gần bằng $188.5~cm^2, 301.6~cm^2, 301.6~cm^3$ II. Hình nón cụt#1. Hình nón cụt là hình gì?Đinh nghĩa: Hình nón cụt là hình có hai đáy là 2 hình tròn có bán kính to nhỏ khác nhau nằm trên hai mặt phẳng song song, có đường nối tâm là trục đối xứng.
Như các bạn có thể thấy ở hình bên dưới: Khi cắt hình nón bởi một mặt phẳng song song với mặt phẳng đáy (hình tròn đáy) chúng ta sẽ thu được một hình nón cụt. 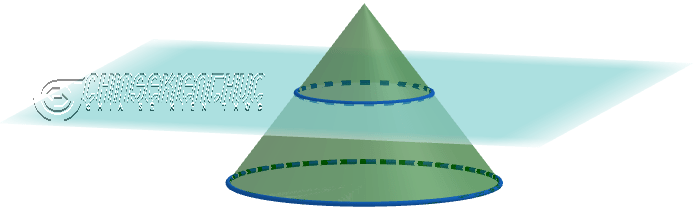 #2. Cách tính diện tích xung quanh của hình nón cụtDiện tích xung quanh của hình nón cụt sẽ bằng tích của $\pi$, tổng độ dài hai bán kính, độ dài đường sinh Công thức: $S_{xq}=\pi.(r_1+r_2).l$ #3. Cách tính diện tích toàn phần của hình nón cụtDiện tích toàn phần của hình nón cụt sẽ bằng tổng của diện tích xung quanh, diện tích đáy lớn, diện tích đáy bé Công thức: $S_{tp}=S_{xq}+\pi(r_1^2+r_2^2)= \pi.(r_1+r_2).l +\pi.(r_1^2+r_2^2)$
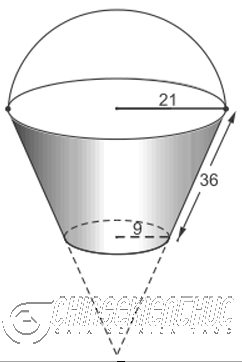
#3. Cách tính thể tích của hình nón cụtThể tích của hình nón cụt sẽ bằng / được tính theo công thức $\frac{1}{3}.\pi.h.(r_1^2+r_2^2+r_1.r_2)$ Công thức: $V=\frac{1}{3}.\pi.h.(r_1^2+r_2^2+r_1.r_2)$ Ví dụ 2: Cho một cái xô có dạng hình nón cụt với các kích thước như Hình 1
Lời Giải: 2.1. Diện tích xung quanh của xôTrước hết ta thấy diện tích xung quanh của xô chính bằng diện tích xung quanh của hình nón cụt. Mà diện tích xung quanh của hình nón cụt lại bằng diện tích xung quanh của hình nón lớn trừ diện tích xung quanh của hình nón nhỏ. + Diện tích hình nón lớn: Gọi Áp dụng định lí Ta-lét ta được: $\frac{l}{l-36}=\frac{21}{9} \Rightarrow l=63~cm$ => Suy ra diện tích xung quanh của hình nón lớn sẽ bằng $\pi.21.63=1323\pi \approx 4156.3~cm^2$ + Diện tích hình nón nhỏ Gọi Ta có $l'+36=l \Leftrightarrow l'+36=63 \Leftrightarrow l'=27~cm$ Suy ra diện tích xung quanh của hình nón nhỏ sẽ bằng $\pi.9.27=243\pi \approx 763.4~cm^2$ => Vậy diện tích xung quanh của hình nón cụt sẽ bằng $1323\pi – 243\pi=1080\pi \approx 3392.9~cm^2$ 2.2. Dung tích của xô khi đầyTrước hết ta thấy dung tích của xô khi chứa đầy nước bằng thể tích của hình nón cụt Mà thể tích của hình nón cụt lại bằng thể tích của hình nón lớn trừ thể tích của hình nón nhỏ + Thể tích của hình nón lớn: Chiều cao của hình nón lớn sẽ bằng $\sqrt{63^2-21^2}=42\sqrt{2} \approx 59.4~cm$ Suy ra thể tích của hình nón lớn sẽ bằng $\frac{1}{3}.\pi.21^2.42\sqrt{2} \approx 27430.4~cm^3$ + Thể tích của hình nón nhỏ: Chiều cao của hình nón nhỏ sẽ bằng $\sqrt{27^2-9^2}=18\sqrt{2} \approx 25.5~cm$ Suy ra thể tích của hình nón nhỏ sẽ bằng $\frac{1}{3}.\pi.9^2.18\sqrt{2} \approx 2159.3~cm^3$ Vậy thể tích của hình nón cụt sẽ bằng $\frac{1}{3}.\pi.21^2.42\sqrt{2}-\frac{1}{3}.\pi.9^2.18\sqrt{2} \approx 25271.1~cm^3$ Vậy diện tích xung quanh của xô, dung tích của xô khi chứa đầy nước lần lượt gần bằng $3392.9~cm^2, 25271.1~cm^3$ Nhận xét:
III. Lời kếtOkay, như vậy là qua bài viết này bạn đã biết cách tích diện tích hình nón, diện tích hình nón cụt, thể tích hình nón và thể tích hình nón cụt rồi nhé. Như các bạn đã biết, Toán học bắt nguồn từ thực tiễn, Toán học giúp giải quyết các vấn đề trong thực tiễn. Tuy nhiên, việc ứng dụng được kiến thức Toán học thuần túy vào thực tiễn không hề dễ dàng. Bạn cần có thời gian để hiểu kỹ mảng kiến thức đó và phải biết cách chuyển từ bài toán thực tiễn sang bài toán thuần túy. Trở lại
Okay, hi vọng là những kiến thức trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ! Đọc thêm: CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé ! |
| You are subscribed to email updates from Blog chia sẻ kiến thức: Máy tính - Công nghệ & Cuộc Sống. To stop receiving these emails, you may unsubscribe now. | Email delivery powered by Google |
| Google, 1600 Amphitheatre Parkway, Mountain View, CA 94043, United States | |

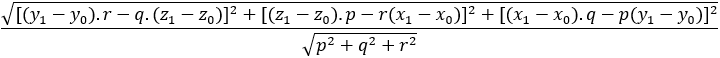






0 nhận xét:
Đăng nhận xét