7 cách giải phương trình bậc hai đơn giản, hiệu quả |
- 7 cách giải phương trình bậc hai đơn giản, hiệu quả
- 5 phương pháp giải hệ hai phương trình bậc nhất hai ẩn
- Tính khoảng cách giữa 2 đường thẳng chéo nhau bằng CASIO
| 7 cách giải phương trình bậc hai đơn giản, hiệu quả Posted: 19 Apr 2022 04:42 AM PDT Mến chào tất cả các bạn, hôm này mình sẽ hướng dẫn cho các bạn cách giải phương trình bậc hai bất kì bằng 7 cách khác nhau. Tha hồ cho các bạn chọn lựa. Mỗi một cách sẽ có một số ưu điểm và khuyết điểm riêng, tùy thuộc vào phương trình cụ thể mà chúng ta sẽ cân nhắc lựa chọn sử dụng cho phù hợp. Hãy linh hoạt nha các bạn ! Trong 7 cách này có cách chỉ có thể áp dụng cho phương trình bậc hai, có cách có thể áp dụng cho phương trình bậc 2, 3, 4. Đặc biệt, có cách có thể áp dụng cho phương trình bậc Okay, ngay bây giờ chúng ta cùng tìm hiểu thôi nào … Mục Lục Nội Dung I. Định nghĩa phương trình bậc haiPhương trình bậc hai là phương trình có dạng $ax^2+bx+c=0$ với điều kiện là $a \neq 0$ Phương trình $x^2+2x-3=0$ là một phương trình bậc hai II. 7 cách giải phương trình bậc hai#1. Tính biệt thức DeltaĐây là phương pháp được nhiều người sử dụng nhất, việc áp dụng rất đơn giản, bạn chỉ cần nhớ công thức là được thôi. Lời Giải: $\Delta=b^2-4.a.c=2^2-4.1.(-3)=16$ Vì $\Delta>0$ nên phương trình đã cho có hai nghiệm phân biệt:
=> Vậy phương trình đã cho có hai nghiệm phân biệt là 1, -3 Chú ý:
#2. Tính biệt thức Delta'Phương pháp này nên được sử dụng khi Phương pháp này rất có ích khi các hệ số a, b, c có giá trị lớn. Lời Giải: Dễ thấy $b'=\frac{b}{2}$ hay $b'=\frac{2}{2}=1$ $\Delta'=b'^2-a.c=1^2-1.(-3)=4$ Vì $\Delta' > 0$ nên phương trình đã cho có hai nghiệm phân biệt
Vậy phương trình đã cho có hai nghiệm phân biệt là 1, -3 Chú ý:
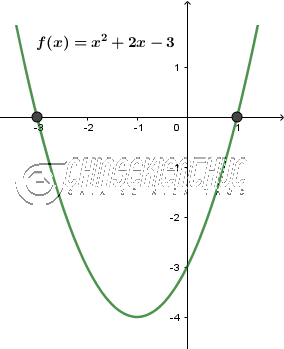
#3. Hệ quả của định lý ViètePhương pháp này nếu áp dụng được sẽ giúp chúng ta tiết kiệm được khá nhiều thời gian và công sức để giải bài, tuy nhiên việc áp dụng trong thực tế khá hạn chế. Lời Giải: Vì $a+b+c=0$ hay $1+2+(-3)=0$ nên phương trình đã cho có một nghiệm là 1 và nghiệm còn lại là $\frac{c}{a}=\frac{-3}{1}=-3$ => Vậy phương trình đã cho có hai nghiệm phân biệt là 1, -3 Chú ý: Nếu $a-b+c=0$ thì phương trình có một nghiệm là -1 và nghiệm còn lại là $-\frac{c}{a}$ #4. Nhẩm nghiệmTrước hết các bạn nên nhớ đa thức $f(x)=ax^2+bx+c$ với điều kiện $a \neq 0$ và $a, b, c$ là những số nguyên
Thực ra phương pháp này là trường hợp mở rộng của phương pháp hệ quả của định lý Viète bên trên. Lời Giải: Vì $a=1, b=2, c=-3$ là những số nguyên nên chúng ta có thể áp dụng phương pháp này: Đặt $f(x)=x^2+2x-3$ -3 có các ước -1, 1, -3, 3 Nếu phương trình có nghiệm nguyên thì chỉ có thể là các số -1, 1, -3, 3
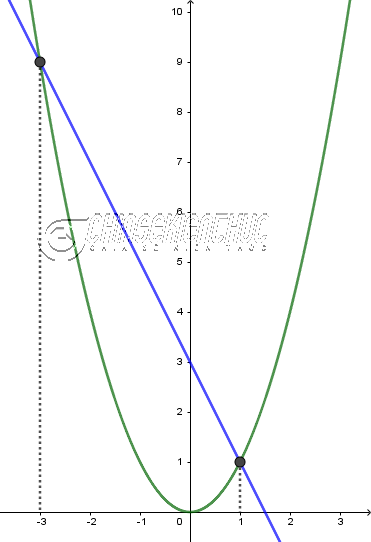
=> Vậy phương trình đã cho có hai nghiệm phân biệt là 1, -3 Chú ý: Vì phương trình bậc hai có tối đa hai nghiệm nên mình không cần kiểm tra 3 (3 chắc chắn không phải là nghiệm của phương trình đã cho) #5. Phương pháp đồ thịPhương pháp đồ thị có thể áp dụng được cho phương trình bậc 2, 3 và 4. Điều kiện là bạn phải vẽ được đồ thị của chúng. Ngoài ra, phương pháp này chỉ khả dụng khi nghiệm là những số nguyên. Lời Giải: Phương trình đã cho tương được với $x^2=-2x+3$ Đặt $f(x)=x^2$ và $g(x)=-2x+3$ Vẽ
Hoành độ giao điểm của đồ thị hàm số Quan sát đồ thị ta dễ dàng nhận thấy hoành độ của hai giao điểm lần lượt là Dự đoán 1 và -3 là nghiệm của phương trình Thay 1 và -3 lần lượt vào phương trình đã cho $1^2+2.1-3=0$ và $(-3)^2+2.(-3)-3=0$ (thỏa mãn) => Vậy phương trình đã cho có hai nghiệm phân biệt là 1, -3 Chú ý: Ở đây mình chọn cách này để học sinh Trung học cơ sở vẫn có thể hiểu được. Trường hợp bạn có thể vẽ được đồ thị của hàm số bậc hai dạng đầy đủ tức $ax^2+bx+c$ thì bạn không cần phải vẽ hai đồ thị. Lúc bấy giờ hoành độ giao điệm của đồ thị với trực hoành chính là nghiệm của phương trình.
#6. Phương pháp máy tính CASIO fx-580VN XNhư mình đã nói bên trên, phương pháp này chỉ nên sử dụng khi cần kiểm tra kết quả hoặc làm bài kiểm tra / bài thi trắc nghiệm Lời Giải: Bước 1. Chọn phương thức tính toán
Bước 2. Chọn
Bước 3. Chọn bậc
Bước 4. Lần lượt nhập các hệ số …
Bước 5. Nhấn phím
Chú ý: Nhắc lại lần nữa, phương pháp này có thể tìm được nghiệm của phương trình bậc 2, 3 và 4 nha các bạn.
#7. Phương pháp biến đổi tổng quátPhương pháp này chủ yếu để rèn luyện khả năng tư duy, tính toán, tìm nghiệm trong trường hợp tổng quát, biện luận nghiệm, … Lời Giải: $x^2+2x-3=0 \Leftrightarrow \left(\frac{x^2}{x}+\frac{2x}{2x}\right)^2-\left(\frac{2x}{2x}\right)^2-3=0 \Leftrightarrow (x+1)^2-(1)^2-3=0 \Leftrightarrow (x+1)^2=4$ $\Leftrightarrow \sqrt{(x+1)^2}= \sqrt{4} \Leftrightarrow |x+1|=2$ $\Leftrightarrow \left[\begin{array}{}x+1=2 \\ x+1=-2 \end{array}\right. \Leftrightarrow \left[\begin{array}{}x=1 \\ x=-3 \end{array}\right.$ Chú ý:
III. Lời kếtVâng, trên đây là 7 cách giải phương trình bậc 2 mà mình đã tổng hợp lại cho các bạn tiện theo dõi. Hãy linh hoạt để áp dụng, nó sẽ giúp bạn tiết kiệm rất nhiều thời gian làm bài tập đấy.
Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ! Đọc thêm: CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé ! |
| 5 phương pháp giải hệ hai phương trình bậc nhất hai ẩn Posted: 19 Apr 2022 04:40 AM PDT Xin chào tất cả các bạn, hôm này mình sẽ hướng dẫn cho các bạn 5 cách giải hệ hai phương trình bậc nhất hai ẩn, nắm được 5 phương pháp này thì bạn sẽ không phải "ngại" bất kỳ trường hợp nào cả. Cụ thể thì chúng ta sẽ có: Phương pháp cộng, phương pháp thế, phương pháp đồ thị, phương pháp cao cấp (ma trận nghịch đảo, định thức) và phương pháp sử dụng máy tính CASIO. Trong đó, 3 phương pháp đầu tiên là dành cho học sinh Trung học, phương pháp thứ tư dành cho sinh viên, còn riêng phương pháp sử dụng máy tính CASIO mang tính chất hỗ trợ, kiểm tra kết quả là chính. Mục Lục Nội Dung I. Định nghĩa về hệ hai phương trình bậc nhất hai ẩnHệ hai phương trình bậc nhất 2 ẩn có dạng $\left\{\begin{array}{ll}ax+by&=c \\ a'x+b'y&=c'\end{array}\right.$
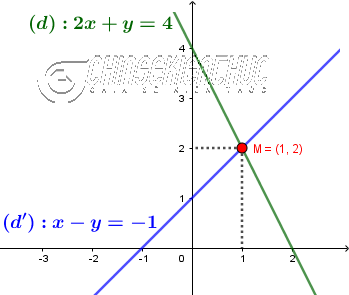
Chẳng hạn $\left\{\begin{array}{ll}2x+y&=4 \\ x-y&=-1\end{array}\right.$ là hệ hai phương trình bậc nhất hai ẩn #1. Sử dụng phương pháp cộngPhương pháp này nên sử dụng khi hệ phương trình có $a+a'=0$ hoặc $b+b'=0$ Quan sát hệ phương trình đã cho ta thấy $b+b'=0$ cụ thể $1+(-1)=0$ Lời Giải: $\left\{\begin{array}{ll}2x+y&=4 \\ x-y&=-1\end{array}\right.$ $\Leftrightarrow \left\{\begin{array}{ll}3x&=3 \\ x-y&=-1\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}x&=1 \\ x-y&=-1\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}x&=1 \\ 1-y&=-1\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}x&=1 \\ y&=2\end{array}\right.$ Vậy nghiệm của hệ phương trình đã cho là (1; 2) #2. Phương pháp thế
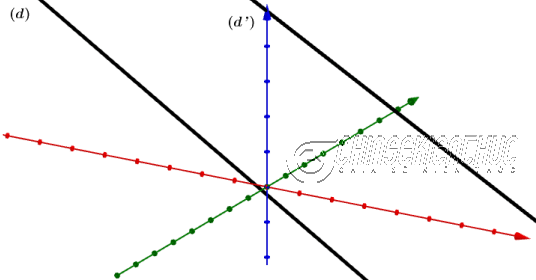
Đối với hệ phương trình này mình sẽ chọn phương trình thứ nhì $x-y=-1$ và biểu diễn x theo y Lời Giải: $\left\{\begin{array}{ll}2x+y&=4 \\ x-y&=-1\end{array}\right.$ $\Leftrightarrow \left\{\begin{array}{ll}2x+y&=4 \\ x&=-1+y\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}2(-1+y)+y&=4 \\ x&=-1+y\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}y&=2 \\ x&=-1+y\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}y&=2 \\ x&=1 \end{array}\right.$ => Vậy nghiệm của hệ phương trình đã cho là (1; 2) #3. Phương pháp đồ thịPhương pháp đồ thị chỉ nên sử dụng khi các hệ số là những số nguyên nha các bạn. Lời Giải: Gọi hai đường thẳng xác định bởi hai phương trình trong hệ đã cho lần lượt là $(d): 2x+y=4$ và $(d'): x-y=-1$ Vẽ
Dự đoán (1; 2) là nghiệm của hệ phương trình đã cho. Thay $x=1, y=2$ vào hệ phương trình $\left\{\begin{array}{ll}2.1+2&=4 \\ 1-2&=-1\end{array}\right.$ Ta thấy (1; 2) thỏa mãn => Vậy nghiệm của hệ phương trình đã cho là (1; 2) #4. Phương pháp cao cấpĐặt $A=\left(\begin{array}{ll}a&b \\ a'&b'\end{array}\right)$ Phương pháp này chỉ có thể sử dụng khi $|A| \neq 0$ 4.1. Ma trận nghịch đảoDễ thấy $A=\left(\begin{array}{cc}2&1 \\ 1&-1\end{array}\right)$ Vì $|A|=2(-1)-1.1=-3 \neq 0$ nên A khả nghịch Ma trận nghịch đảo của ma trận A sẽ bằng $A^{-1}=\left(\begin{array}{cc}\frac{1}{3}&\frac{1}{3} \\ \frac{1}{3}&-\frac{2}{3}\end{array}\right)$ Suy ra $\left(\begin{array}{}x\\y\end{array}\right)=\left(\begin{array}{cc}\frac{1}{3}&\frac{1}{3} \\ \frac{1}{3}&-\frac{2}{3}\end{array}\right) \left(\begin{array}{}4\\-1\end{array}\right) \Leftrightarrow \left(\begin{array}{}x\\y\end{array}\right) =\left(\begin{array}{}1\\2\end{array}\right)$ => Vậy nghiệm của hệ phương trình đã cho là (1; 2) 4.2. Định thứcDễ thấy $A=\left(\begin{array}{cc}2&1 \\ 1&-1\end{array}\right)$ Vì $|A|=2(-1)-1.1=-3 \neq 0$ nên hệ phương trình đã cho có một nghiệm duy nhất
Suy ra $x=\frac{|A_1|}{|A|}=\frac{-3}{-3}=1$ và $y=\frac{|A_2|}{|A|}=\frac{-6}{-3}=2$ => Vậy nghiệm của hệ phương trình đã cho là (1; 2) #5. Phương pháp máy tính CASIO fx-580VN XBước 1. Chọn phương thức tính toán
Bước 2. Chọn
Bước 3. Nhập số
Bước 4. Nhập số các hệ số …
Bước 5. Nhấn phím
=> Vậy nghiệm của hệ phương trình đã cho là (1; 2)
II. Lời kếtOkay, trên đây là 5 phương pháp giải hệ hai phương trình bậc nhất hai ẩn mà mình đã tổng hợp lại. Tùy thuộc vào hệ phương trình cụ thể mà chúng ta sẽ cân nhắc lựa chọn phương pháp cho phù hợp nhất.
Hi vọng những kiến thức mình chia sẻ trong bài hướng dẫn này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ! Đọc thêm: CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé ! |
| Tính khoảng cách giữa 2 đường thẳng chéo nhau bằng CASIO Posted: 19 Apr 2022 04:37 AM PDT Xin chào tất cả các bạn, hôm nay mình sẽ hướng dẫn các bạn cách tính khoảng cách giữa hai đường thẳng chéo nhau. Về cơ bản thì chúng ta sẽ có 2 hướng để tiếp cận: Một là dựa vào tích có hướng (note) và tích vô hướng, hai nữa là dựa vào ma trận. Trong bài viết này mình sẽ tiếp cận theo hướng thứ 2, tức là dựa vào ma trận. Cụ thể hơn là ma trận $2 \times 2$ và $3 \times 3$ Việc tiếp cận theo hướng này sẽ gây ra chút khó khăn cho các bạn học sinh, tuy nhiên trắc nghiệm đang là xu hướng và máy tính CASIO ngày càng có nhiều tính năng hữu ích hơn => vậy nên khó khăn trên sẽ không hề đáng ngại phải không nào. Mục Lục Nội Dung #1. Công thức tính khoảng cách giữa hai đường thẳng chéo nhauTrong không gian $Oxyz$ cho hai đường thẳng chéo nhau $(d)$ và $(d')$. Tính khoảng cách giữa hai đường thẳng trên biết …
Khoảng cách giữa hai đường thẳng $(d)$ và $(d')$ được xác định bởi công thức: $\frac{\left|\left|\begin{array}{ccc} a_1 & b_1 & c_1 \\ a_1′ & b_1′ & c_1′ \\ x_0′-x_0 & y_0′-y_0 & z_0′-z_0 \end{array}\right|\right|}{\sqrt{\left|\begin{array}{ll} b_1 & c_1 \\ b_1′ & c_1′ \end{array}\right|^2+\left|\begin{array}{ll} c_1 & a_1 \\ c_1′ & a_1′ \end{array}\right|^2+\left|\begin{array}{ll} a_1 & b_1 \\ a_1′ & b_1′ \end{array}\right|^2}}$
#2. Tìm hiểu thêm về cách chứng minh công thức
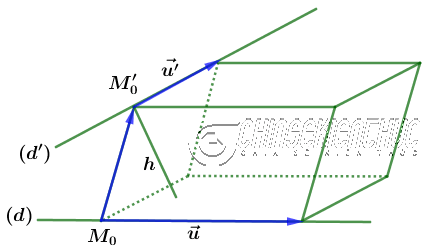
Gọi Lúc bấy giờ Gọi $S$ là diện tích của hình bình hành tạo bởi $\vec{u}, \vec{u'}$ Lúc bấy giờ S được tính theo công thức $[\vec{u}; \vec{u'}]=\sqrt{\left|\begin{array}{ll} b_1 & c_1 \\ b_1′ & c_1′ \end{array}\right|^2+\left|\begin{array}{ll} c_1 & a_1 \\ c_1′ & a_1′ \end{array}\right|^2+\left|\begin{array}{ll} a_1 & b_1 \\ a_1′ & b_1′ \end{array}\right|^2}$ => Suy ra chiều của $h$ của hình hộp cũng chính là khoảng cách giữa hai đường thẳng chéo nhau và $h=\frac{V}{S}$ #3. Cách tính định thức của ma trận3.1. Ma trận 2 x 2Định thức của ma trận $A=\left(\begin{array}{ll}a&b\\c&d\end{array}\right)$ sẽ được tính theo công thức $a.d-c.b$ Chú ý: Định thức của ma trận A thường được kí hiệu là |A| hoặc Det(A) 3.2. Ma trận 3 x 3Định thức của ma trận $B=\left(\begin{array}{lll}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right)$ sẽ được tính theo công thức $a_{11}\left|\begin{array}{ll}a_{22}&a_{23}\\a_{32}&a_{33}\end{array}\right|-a_{12}\left|\begin{array}{ll}a_{21}&a_{23}\\a_{31}&a_{33}\end{array}\right|+a_{13}\left|\begin{array}{ll}a_{21}&a_{22}\\a_{31}&a_{32}\end{array}\right|$ #4. Ví dụ minh họaTính khoảng cách giữa hai đường thẳng chéo nhau $(d):\frac{x}{2}=\frac{y-1}{1}=\frac{z+1}{-2}$ và $(d'):\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{-2}$
Lời Giải: Dễ thấy …
Suy ra $\overrightarrow{M_0M_0′}=(1; 1; 4)$ => Vậy khoảng cách giữa $(d)$ và $(d')$ là: $\frac{\left|\left|\begin{array}{lll} 2 & 1 & -2 \\ 1 & 2 & -2 \\ 1 & 1 & 4 \end{array}\right|\right|}{\sqrt{\left|\begin{array}{ll} 1 & -2 \\ 2 & -2 \end{array}\right|^{2}+\left|\begin{array}{ll} -2 & 2 \\ -2 & 1 \end{array}\right|^{2}+\left|\begin{array}{ll} 2 & 1 \\ 1 & 2 \end{array}\right|^{2}}}=\frac{16\sqrt{17}}{17}$
#5. Thủ thuật tính nhanh bằng máy tính CASIO fx-580VN XBước 1. Chọn phương thức tính toán
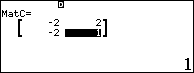
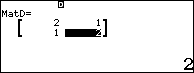
Bước 2. Lần lượt gán bốn ma trận vào
Bước 3. Tính giá trị biểu thức (Abs(Det(MatA))) ⨼(√((Det(MatB))2+(Det(MatC))2+(Det(MatD))2))
Chú ý #6. Lời kếtOkay, đó là cách tính khoảng cách giữa hai đường thẳng chéo nhau mà theo mình là tối ưu nhất cho phần thi trắc nghiệm toán. Nếu bạn là sinh viên thì cho dù câu hỏi được cho dưới dạng trắc nghiệm hay là tự luận đều không thành vấn đề, vì các bạn đã được học về ma trận trong chương trình Toán cao cấp hoặc Đại số tuyến tính. Còn nếu bạn là học sinh và …
Hi vọng là bài viết sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ! CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé ! |
| You are subscribed to email updates from Blog chia sẻ kiến thức: Máy tính - Công nghệ & Cuộc Sống. To stop receiving these emails, you may unsubscribe now. | Email delivery powered by Google |
| Google, 1600 Amphitheatre Parkway, Mountain View, CA 94043, United States | |


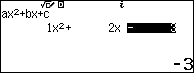
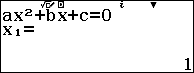
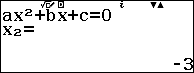
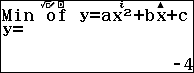


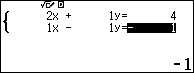


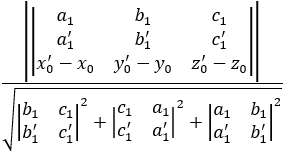
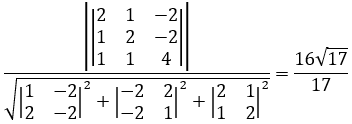





0 nhận xét:
Đăng nhận xét