Tam giác Pascal là gì? Bài tập ví dụ về tam giác Pascal |
- Tam giác Pascal là gì? Bài tập ví dụ về tam giác Pascal
- Hằng đẳng thức là gì? 7 hằng đẳng thức đáng nhớ (có ví dụ)
- 3 cách chứng minh tam giác đồng dạng, có ví dụ dễ hiểu
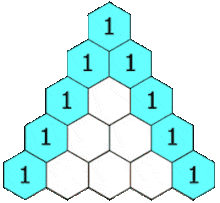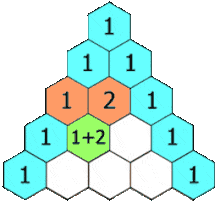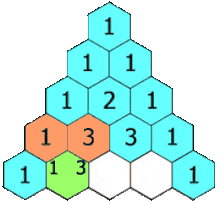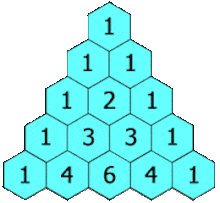
| Tam giác Pascal là gì? Bài tập ví dụ về tam giác Pascal Posted: 29 Apr 2022 07:46 PM PDT Khai triển đa thức là biến đổi một đa thức ở dạng tích các tổng, hoặc hiệu thành dạng tổng, hoặc hiệu các tích. Khai triển đa thức là một trong những kiến thức cơ bản của môn Đại số mà ngay từ những năm Trung học cơ sở chúng ta đã được học Trong rất nhiều bài toán chúng ta cần thực hiện thao tác khai triển mới có thể tìm ra đáp án, tiêu biểu như rút gọn biểu thức, rút gọn phân thức, giải phương trình, tính giới hạn, đạo hàm, tích phân, … Về cơ bản thì quá trình khai triển không có gì khó khăn cả, nhưng khai triển sao cho nhanh chóng và chính xác thì không phải ai cũng làm được. Có khá nhiều cách giúp chúng ta khai triển đa thức nhanh chóng và chính xác, trong đó dựa vào tam giác Pascal là một trong những cách phổ biến nhất. Và đó cũng là nội dung chính trong bài viết này. Mục Lục Nội Dung #1. Tam giác Pascal là gì?Tam giác Pascal là một mảng tam giác của các hệ số nhị thức. Các con số được sắp xếp để chúng phản ánh như một hình tam giác. Tam giác Pascal được đặt tên theo tên của nhà Toán học đã tìm ra nó (Blaise Pascal).  #2. Cách xây dựng tam giác PascalBước 1. Dòng thứ nhất viết một con số
Bước 2. Dòng thứ 2, viết hai con số
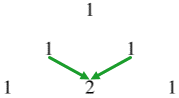
Bước 3. Dòng thứ ba … a) Ở vị trí đầu dòng và cuối dòng viết số
b) Số ở chính giữa bằng tổng của hai số ở dòng thứ
Bước 4. Dòng thứ 4, dòng thứ 5, dòng thứ 6, …, thực hiện tương tự
Một số lưu ý:
Nếu xem tam giác Pascal là một tam giác cân thì hai cạnh bên luôn được tạo thành từ những con số 1 Tam giác trên có 7 dòng tương ứng với bậc 6, một cách dễ hiểu hơn là tam giác trên có thể sử dụng để khai triển biểu thức $(ax \pm by)^n$ với n tối đa bằng 6 #3. Ứng dụng tam giác Pascal trong giải toán như thế nào?Hầu hết chúng ta đều sử dụng tam giác Pascal để khai triển các nhị thức, tức là các biểu thức có dạng $(ax \pm by)^n$ Chẳng hạn như: $(x+y)^2, (x-y)^3, (2x+3y)^2, \left(\frac{2}{3}x-\frac{5}{7}y\right)^3$ Chú ý:
#4. Bài tập ví dụ minh họa tam giác PascalVí dụ 1. Khai triển nhị thức $(x+y)^2$ >Cách tư duy: Bước 1. Xác định dấu và hệ số của các hạng tử.
$+1+2+1$ Bước 2. Biểu diễn x, bậc của x sẽ giảm dần từ 2 đến 0 $+1x^2+2x^1+1x^0$ Bước 3. Biểu diễn y, bậc của y sẽ tăng dần từ 0 đến 2 $+1x^2y^0+2x^1y^1+1x^0y^2$ Bước 4. Rút gọn biểu thức $+1x^2y^0+2x^1y^1+1x^0y^2=x^2+2xy+y^2$ Vậy $(x+y)^2=x^2+2xy+y^2$ Trình bày lời giải: $(x+y)^2=+1x^2y^0+2x^1y^1+1x^0y^2=x^2+2xy+y^2$ Một số lưu ý:
Ví dụ 2. Khai triển nhị thức $(x-y)^3$
Lời giải: $(x-y)^3=+1x^3y^0-3x^2y^1+3x^1y^2-1x^0y^3=x^3+3x^2y+3xy^2+y^3$ Ví dụ 3. Khai triển nhị thức $(2x+3y)^2$
Lời giải: $(2x+3y)^2=+1(2x)^2(3y)^0+2(2x)^1(3y)^1+1(2x)^0(3y)^2=4x^2+12xy+9y^2$ Ví dụ 4. Khai triển nhị thức $\left(\frac{2}{3}x-\frac{5}{7}y\right)^3$
Lời giải: $\left(\frac{2}{3}x-\frac{5}{7}y\right)^3$ $=+1\left(\frac{2}{3}x\right)^3\left(\frac{5}{7}y\right)^0-3\left(\frac{2}{3}x\right)^2\left(\frac{5}{7}y\right)^1+3\left(\frac{2}{3}x\right)^1\left(\frac{5}{7}y\right)^2-1\left(\frac{2}{3}x\right)^0\left(\frac{5}{7}y\right)^3$ $=\frac{8}{27} x^{3}-\frac{20}{21} x^{2} y+\frac{50}{49} x y^{2}-\frac{125}{343} y^{3}$ Ví dụ 5. Khai triển đa thức $(2x+3y-5z)^2$ Nhận xét $(2x+3y-5z)^2$ không phải là một nhị thức nhưng nếu biết cách sử dụng linh hoạt chúng ta vẫn có thể dựa vào tam giác Pascal để hỗ trợ quá trình khai triển Cách 1: Sử dụng tam giác Pascal $(2x+3y-5z)^2=[(2x+3y)-5z]^2$
Lời giải: $[(2x+3y)-5z]^2$ $=+1(2x+3y)^2(5z)^0-2(2x+3y)^1(5z)^1+1(2x+3y)^0(5z)^2$ $=(2x+3y)^2-2(2x+3y)(5z)+25z^2$ Vì $(2x+3y)^2=4x^2+12xy+9y^2$ nên … $=(4x^2+12xy+9y^2)-2(2x+3y)(5z)+25z^2$ $=4 x^{2}+12 x y-20 x z+9 y^{2}-30 y z+25 z^{2}$ Cách 2: Sử dụng hằng đẳng thức Để khai triển nhanh đa thức $(2x+3y-5z)^2$ bạn có thể sử dụng hằng đẳng thức $(a+b-c)^2=a^{2}+2 a b-2 a c+b^{2}-2 b c+c^{2}$ Ở đây a, b, c trong công thức sẽ lần lượt bằng 2x, 3y, 5z $(2x+3y-5z)^2$ $=(2x)^2+2(2x)(3y)-2(2x)(5z)+(3y)^2-2(3y)(5z)+(5z)^2$ $=4 x^{2}+12 x y-20 x z+9 y^{2}-30 y z+25 z^{2}$ Cách 3: Nhân đa thức với đa thức Cách này rất tốn thời gian nên mình không khuyến khích sử dụng, chỉ sử dụng khi bạn quên mất cách lập tam giác Pascal và quên luôn hằng đẳng thức $(a+b-c)^2$ $(2x+3y-5z)^2$ $=(2x+3y-5z)(2x+3y-5z)$ $=2x.2x+2x.3y-2x.5z+3y.2x+3y.3y-3y.5z-5z.2x-5z.3y+5z.5z$ $=4 x^{2}+12 x y-20 x z+9 y^{2}-30 y z+25 z^{2}$ #5. Lời kếtNhư vậy tam giác Pascal sẽ giúp chúng ta khai triển nhanh các biểu thức có dạng $(ax \pm by)^2$ hoặc các biểu thức có dạng gần gần như vậy. Tương tự như các phương pháp khác, phương pháp này cũng có một số nhược điểm nhất định, đó là:
Để khắc phục 2 nhược điểm trên bạn có thể tìm hiểu về thêm nhị thức Newton trên Wikipedia nhé. Hi vọng bài viết này sẽ hữu ích với bạn, xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ! Đọc thêm: CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé ! |
| Hằng đẳng thức là gì? 7 hằng đẳng thức đáng nhớ (có ví dụ) Posted: 29 Apr 2022 07:20 PM PDT Xin chào tất cả các bạn, hôm nay chúng ta sẽ cùng nhau tìm hiểu về các hằng đẳng thức đáng nhớ và những ứng dụng cơ bản của chúng. Đầu tiên mình sẽ trình bày về định nghĩa, sau đó sẽ liệt kê ra một số ứng dụng tiêu biểu, liệt kê ra các hằng đẳng thức (cơ bản, mở rộng và tổng quát) và cuối cùng là cho ví dụ minh họa. Thế đã ok chưa nhỉ 🙂 Trong bốn phần vừa giới thiệu thì phần liệt kê các hằng đẳng thức và ví dụ minh họa là quan trọng nhất, các bạn nhớ dành nhiều thời gian cho phần nội dung này nhé. Mục Lục Nội Dung I. Hằng đẳng thức là gì?Trước khi tìm hiểu định nghĩa về hằng đẳng thức thì chúng ta cần định nghĩa đẳng thức trước. Như vậy các bạn sẽ hiểu rõ về bản chất hơn ! Đẳng thức là cặp biểu thức nối liền với nhau bởi dấu Hằng đẳng thức là đẳng thức đúng với mọi trị số gán cho các chữ trong đó. Còn theo Wikipedia định nghĩa thì: Hằng đẳng thức nghĩa là một loạt các đẳng thức có liên quan tới nhau, hợp lại thành một hằng đẳng thức. Ví dụ: $(a+b)^2=a^2+2ab+b^2$ là một hằng đẳng thức vì …
Còn $\frac{a+b}{2} \geq \sqrt{ab}$ không là một hằng đẳng thức vì hai biểu thức không được nối với nhau bởi dấu II. Hằng đẳng thức dùng để làm gì?Hằng đẳng thức được ứng dụng rất nhiều trong Toán học, tiêu biểu nhất là …
III. Các hằng đẳng thức đáng nhớCó rất nhiều hằng đẳng thức khác, ở đây mình chỉ liệt kê các hằng đẳng thức thường gặp trong chương trình sách giáo khoa và tạm chia chúng thành ba nhóm. #1. Các hằng đẳng thức cơ bảnCác hằng đẳng thức này rất cơ bản, rất thường gặp khi giải toán, vậy nên bạn cần phải ghi nhớ chúng như ghi nhớ bảng cửu chương nhé.
Chú ý:
#2. Các hằng đẳng thức mở rộngDưới đây là các hằng đẳng thức mở rộng thường gặp, nếu bạn có thể nhớ được các hằng đẳng thức này thì quả là một điều tuyệt vời.
#3. Các hằng đẳng thức tổng quátPhàm cái gì tổng quát thì sẽ khó hiểu và khó nhớ. Tuy nhiên, nếu có thể nhớ và hiểu được thì bạn không cần nhớ các trường hợp cụ thể.
Chú ý
IV. Bài tập ví dụ về hằng đẳng thứcVí dụ 1. Phân tích đa thức $9x^2-6x+1$ thành nhân tử Cách 1:
Lời giải: $9x^2-6x+1=(3x)^2-2(3x).1+1^2=(3x-1)^2$ Cách 2:
Lời giải: Đa thức $9x^2-6x+1$ có một nghiệm kép là $\frac{1}{3}$ => $9x^2-6x+1=9\left(x-\frac{1}{3}\right)\left(x-\frac{1}{3}\right)=9\left(x-\frac{1}{3}\right)^2=(3x-1)^2$ Cách 3: $9x^2-6x+1$ $=9\left(x^2-\frac{6}{9}x+\frac{1}{9}\right)$ $=9\left[\left(\frac{x^2}{x}-\frac{\frac{6}{9}x}{2x}\right)^2-\frac{1}{9}+\frac{1}{9}\right]$ $=9\left[\left(x-\frac{1}{3}\right)^2\right]=9\left(x-\frac{1}{3}\right)^2=(3x-1)^2$ Ví dụ 2. Không giải phương trình hãy tính giá trị biểu thức $A=a^2+b^2$ biết a, b là nghiệm của phương trình $x^2+2x+3=0$ Cách 1:
Lời giải: $A=a^2+b^2=(a+b)^2-2ab$ Áp dụng định lí Viète vào phương trình $x^2+2x+3=0$ ta được hệ thức $\left\{\begin{array}{ll}a+b&=-2\\ab&=3\end{array}\right.$ Suy ra $A=a^2+b^2=(a+b)^2-2ab=(-2)^2-2.3=-2$ Cách 2 (Sử dụng máy tính Casio FX):
Cách giải: Bước 1. Chọn phương thức tính toán
Bước 2. Nhập các hệ số của phương trình …
Bước 3. Nhấn phím
Bước 4. Nhấn phím
Bước 5. Chọn phương thức
Bước 6. Nhập biểu thức $A^2+B^2$ => nhấn phím
Ví dụ 3. Giải hệ phương trình $\left\{\begin{array}{ll}x+y&=2 \\ x^2+y^2&=4\end{array}\right.$ Cách 1:
Lời giải: $\left\{\begin{array}{ll}x+y&=2 \\ x^2+y^2&=4\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}x+y&=2 \\ (x+y)^2-2xy&=4\end{array}\right.$ Đặt $S=x+y, P=xy$ ta được hệ phương trình $\left\{\begin{array}{ll}S&=2 \\ S^2-2P&=4\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}S&=2 \\ 2^2-2P&=4\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}S&=2 \\ P&=0\end{array}\right.$ Theo định lí Viète đảo $x, y$ sẽ là nghiệm của phương trình $X^2-SX+P=0 \Leftrightarrow X^2-2X=0$ Giải phương trình $X^2-2X=0$ ta được hai nghiệm là $X=0, X=2$ => Vậy hệ phương trình đã cho có hai nghiệm là $(0; 2)$ và $(2; 0)$ Cách 2:
Lời giải: $\left\{\begin{array}{ll}x+y&=2 \\ x^2+y^2&=4\end{array}\right.$ $\Leftrightarrow \left\{\begin{array}{ll}x&=2-y \\ (2-y)^2+y^2&=4\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}x&=2-y \\ 2y^2-4y+4&=4\end{array}\right.$ Giải phương trình $2y^2-4y+4=4$ ta được hai nghiệm là $y=0$ và $y=2$
=> Vậy nghiệm của hệ phương trình đã cho là $(2; 0)$ và $(0; 2)$ Cách 3:
Lời giải:
Quan sát hai đồ thị của hàm số ta thấy chúng có hai giao điểm là $A=(0; 2) và B=(2; 0)$ Dự đoán $(0; 2) và $(2; 0)$ là nghiệm của hệ phương trình đã cho Thay $(0; 2) và $(2; 0)$ vào hệ phương trình ta được … $\left\{\begin{array}{ll}0+2&=2 \\ 0^2+2^2&=4\end{array}\right.$ và $\left\{\begin{array}{ll}2+0&=2 \\ 2^2+0^2&=4\end{array}\right.$ Các hệ thức trên đều là ĐÚNG => Vậy $(0; 2) và $(2; 0)$ là nghiệm của hệ phương trình đã cho V. Lời kếtVâng, trên đây là 7 hằng đẳng thức đáng nhớ và các hằng đẳng thức mở rộng quan trọng nhất. Các hằng đẳng thức mà mình vừa trình bày đều đã được chứng minh, nếu muốn chứng minh lại thì bạn có thể biến đổi vế trái thành vế phải (nhân đa thức với đa thức rồi rút gọn). Tuy nhiên mình không khuyến khích các bạn làm như vậy, chỉ tốn thời gian chứ không được lợi ích gì cả. Thay vào đó bạn nên dành thời gian để luyện tập thêm, làm thêm các ví dụ để ghi nhớ và vận dụng thành thạo các hằng đẳng thức đáng nhớ này. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ha ! CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé ! |
| 3 cách chứng minh tam giác đồng dạng, có ví dụ dễ hiểu Posted: 29 Apr 2022 06:56 PM PDT Trong thực tế, chúng ta thường gặp rất nhiều hình có hình dạng giống nhau, nhưng kích thước khác nhau. Những cặp hình như vậy được gọi là đồng dạng (có cùng hình dạng).
Trong Toán học cũng vậy, chúng ta cũng có rất nhiều hình đồng dạng. Tuy nhiên, trong khuân khổ của bài viết này mình sẽ trình trường hợp đồng dạng của tam giác, các hình khác các bạn có thể tự tìm hiểu thêm nếu muốn nhé. Mục Lục Nội Dung I. Hai tam giác đồng dạng là gì?Hai tam giác được gọi là đồng dạng nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
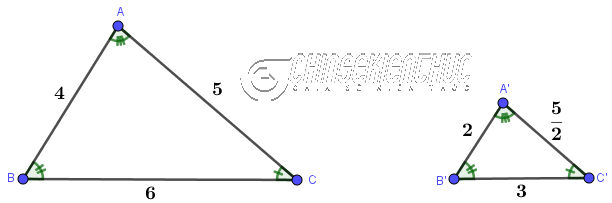
Ví dụ như ở hình bên trên: Tam giác A'B'C' đồng dạng với tam giác ABC vì …
Tam giác A'B'C' đồng dạng với tam giác ABC được kí hiệu là $A'B'C' ∽ ABC$ Chú ý:
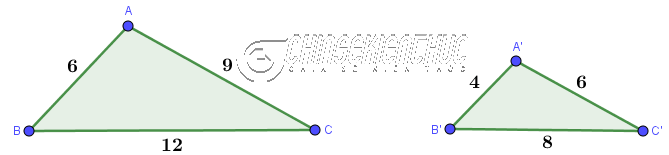
II. Các trường hợp đồng dạng của tam giácĐọc thêm: #1. Trường hợp 2 tam giác đồng dạng thứ nhất: Cạnh – Cạnh – CạnhNếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia, thì hai tam giác đã cho đồng dạng với nhau. Ví dụ 1. Tam giác ABC có đồng dạng với tam giác A'B'C' không? Vì sao? Biết AB=6, BC=12, CA=9; A'B'=4, B'C'=8, C'A'=6
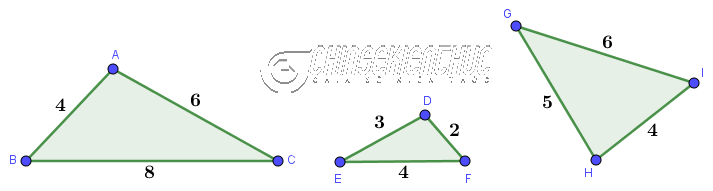
Lời giải: Tam giác ABC đồng dạng với tam giác A'B'C' vì $\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{CA}{C'A'}=\frac{3}{2}$ Ví dụ 2. Cặp tam giác nào trong Hình 1 đồng dạng, không đồng dạng với nhau? Vì sao?
Lời giải: Cặp thứ nhất tam giác ABC và tam giác DFE Tam giác ABC đồng dạng với tam giác DFE vì $\frac{AB}{DF}=\frac{BC}{FE}=\frac{CA}{ED}=\frac{1}{2}$
Cặp thứ 2, tam giác ABC và tam giác HIG Xét tam giác ABC và tam giác HIG
Suy ra $\frac{AB}{HI} \neq \frac{BC}{IG}$ => Vậy tam giác ABC không đồng dạng với tam giác HIG Cặp thứ 3, tam giác DEF và tam giác HGI Xét tam giác DEF và tam giác HGI
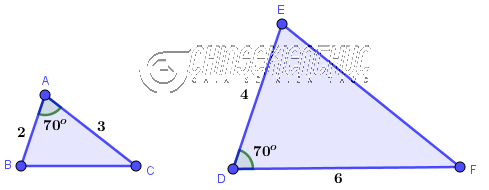
Suy ra $\frac{DE}{HG} \neq \frac{EF}{GI}$ => Vậy tam giác DEF không đồng dạng với tam giác HGI #2. Trường hợp 2 tam giác đồng dạng thứ 2: Cạnh – Góc – CạnhNếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi hai cặp cạnh đó (góc xen giữa cặp cạnh đó) bằng nhau => thì hai tam giác đã cho đồng dạng với nhau. Ví dụ 3. Tam giác ABC có đồng dạng với tam giác DEF không? Vì sao? Biết AB=2, DE=4, CA=3; FD=6, $\widehat{BAC}=\widehat{EDF}=70^o$
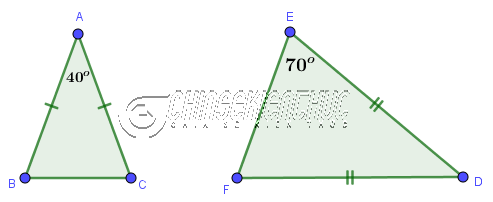
Lời giải: Tam giác ABC đồng dạng với tam giác DEF vì $\frac{AB}{DF}=\frac{CA}{FD}=\frac{1}{2}$ và $\widehat{BAC}=\widehat{EDF}=70^o$ #3. Trường hợp đồng dạng thứ 3: Góc – GócNếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia => thì hai tam giác đã cho đồng dạng với nhau. Ví dụ 4. Chứng minh tam giác ABC đồng dạng với tam giác DEF biết $AB=AC, DE=DF, \hat{A}=40^o, \hat{E}=70^o$
Lời giải: Xét tam giác ABC Ta có $AB=AC$ suy ra tam giác ABC cân tại A (1) Mặc khác ta lại có $\hat{A}=40^o$ (2) Từ (1) và (2) suy ra $\hat{B}=\hat{C}=70^o$ Xét tam giác DEF Ta có $DE=DF$ suy ra tam giác DEF cân tại D (3) Mặc khác ta lại có $\hat{E}=70^o$ (4) Từ (3) và (4) suy ra $\hat{F}=70^o$ Suy ra $\hat{D}=40^o$ Vậy ABC đồng dạng với tam giác DEF (Góc – Góc) III. Lời kếtVâng, như vậy là qua bài viết này thì mình tin là bạn đã hiểu hơn về tam giác đồng dạng rồi đúng không. Không phải ngẫu nhiên mà chúng ta cần đến ba trường hợp đồng dạng, nếu không có ba trường hợp này thì chúng ta sẽ phải chứng minh tam giác đồng dạng dựa vào định nghĩa. Mà việc chứng minh dựa vào định nghĩa tốn khá nhiều thời gian và công sức.Hơn nữa, không phải trường hợp nào chúng ta cũng đủ giả thuyết để chứng minh. Trong Toán học cũng như trong thực tế, không có gì là tự nhiên cả, không có gì là vô dụng cả, tất cả đều có giá trị của nó, nếu chúng ta biết vận dụng đúng cách thì sẽ tiết kiệm được rất nhiều thời gian. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ! CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé ! |
| You are subscribed to email updates from Blog chia sẻ kiến thức: Máy tính - Công nghệ & Cuộc Sống. To stop receiving these emails, you may unsubscribe now. | Email delivery powered by Google |
| Google, 1600 Amphitheatre Parkway, Mountain View, CA 94043, United States | |
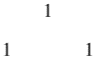


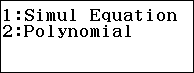

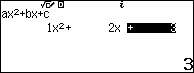
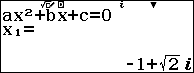

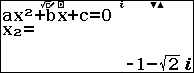

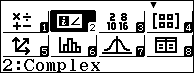



0 nhận xét:
Đăng nhận xét