4 đường thẳng đồng quy trong tam giác, bạn còn nhớ không?

---

• 4 đường thẳng đồng quy trong tam giác, bạn còn nhớ không?
• 4 cách chứng minh hai tam giác vuông bằng nhau (có ví dụ)
• Cách vẽ tam giác đều, tứ giác đều, ngũ giác đều và lục giác đều

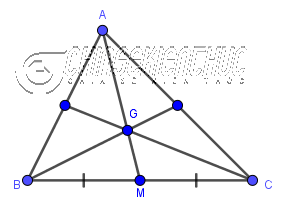
4 đường thẳng đồng quy trong tam giác, bạn còn nhớ không? Posted: 04 Apr 2022 03:03 AM PDT Xin chào tất cả các bạn, hôm nay chúng ta sẽ cùng nhau tìm hiểu về các đường thẳng đồng quy trong tam giác. Về cơ bản thì có bốn loại đường thẳng đồng quy, đó là: đường trung tuyến, đường cao, đường trung trực và đường phân giác. Việc giới thiệu một cách đầy đủ về bốn loại đường trên trong cùng một bài viết là không khả thi, vì vậy mình chỉ phát biểu định nghĩa, vẽ hình minh họa và trình bày một vài kiến thức cơ bản có liên quan trực tiếp mà thôi. Mục đích của bài viết này rất đơn giản, khi đọc đến tên của nó thì bạn có thể vẽ được nó một cách chính xác. Như vậy là rất ok rồi ! Mục Lục Nội Dung #1. Đường trung tuyến của tam giác là gì? + Đường trung tuyến của một tam giác là một đường thẳng đi qua đỉnh và trung điểm của cạnh đối diện. Mỗi tam giác sẽ có 3 đường trung tuyến. Ba đường trung tuyến trong một tam giác luôn đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác. Trọng tâm của tam giác cách đỉnh một khoảng bằng hai phần ba độ dài đường trung tuyến tương ứng. 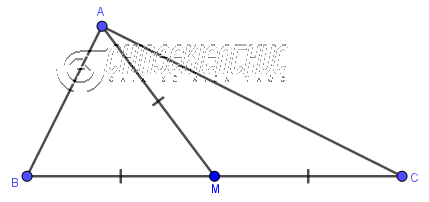AM là đường trung tuyến của tam giác ABC, nó đi qua đỉnh A và trung điểm M của cạnh BC G là trọng tâm của tam giác ABC $AG=\frac{2}{3}AM$ + Trong một tam giác vuông thì độ dài đường trung tuyến ứng với cạnh huyền bằng ½ độ dài cạnh huyền. 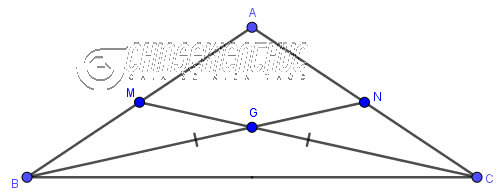AM là đường trung tuyến của tam giác vuông ABC (vuông ở A) nên $AM=\frac{1}{2}BC$ + Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau. Như hình bên trên thì BN, CM là hai đường trung tuyến của tam giác cân ABC (cân ở A) nên BN=CM #2. Đường cao của tam giác là gì? Đường cao của tam giác là một đường thẳng đi qua đỉnh và vuông góc với cạnh đối diện. Hay nói cách khác: Đường cao của một tam giác là đoạn thẳng được kẻ từ một đỉnh và vuông góc với cạnh đối diện của tam giác đó. 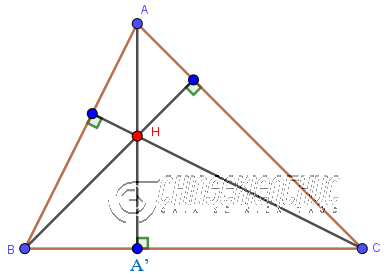Ba đường cao trong một tam giác luôn đồng quy tại một điểm, điểm này được gọi là trực tâm của tam giác. 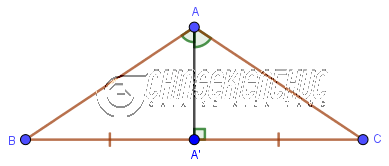AA' là đường cao đi qua đỉnh A và vuông góc với cạnh đối diện BC tại A' G là trực tâm của tam giác ABC + Trong một tam giác cân đường cao đi qua đỉnh cũng là đường trung tuyến, đường trung trực và đường phân giác của tam giác đó. 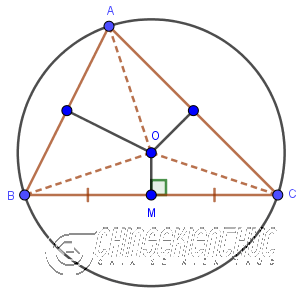Như hình bên trên thì đường cao AA' đi qua đỉnh A của tam giác cân ABC (cân ở A) nên AA' cũng là đường trung tuyến, đường trung trực và đường phân giác. + Trong một tam giác có hai trong bốn loại đường (trung tuyến, đường cao, trung trực, phân giác) trùng nhau thì tam giác đó là tam giác cân => bạn có thể vận dụng kiến thức này vào việc chứng minh tam giác đã cho là tam giác cân. #3. Đường trung trực của tam giác là gì? Đường trung trực của tam giác là đường thẳng đi qua trung điểm của một cạnh và vuông góc với cạnh đó. Ba đường trung trực trong một tam giác luôn đồng quy tại một điểm, điểm này cách đều ba đỉnh của tam giác và là tâm đường tròn ngoại tiếp tam giác. 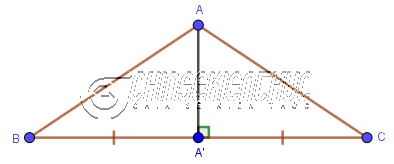OM là đường trung trực tương ứng với cạnh BC O là tâm đường tròn ngoại tiếp tam giác ABC OA = OB = OC + Trong một tam giác cân đường trung trực ứng với cạnh đáy cũng là đường trung tuyến. 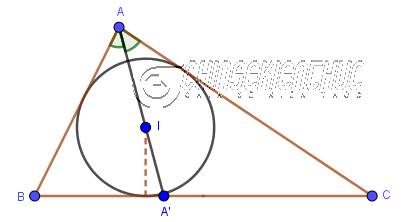Như hình bên trên thì AA' là đường trung trực của tam giác cân ABC (cân tại A) nên cũng là đường trung tuyến #4. Đường phân giác của tam giác là gì? Trước khi đến với khái niệm đường phân giác thì chúng ta sẽ tìm hiểu về khái niệm của tia phân giác trước. Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau. Tia phân giác của $\hat{A}$ cắt cạnh đối diện BC tại điểm A', khi đó AA' được gọi là đường phân giác của $\hat{A}$ Ba đường phân giác trong tam giác luôn đồng quy tại một điểm, điểm này cách đều ba cạnh của tam giác và là tâm đường tròn nội tiếp tam giác AA' là một đường phân giác tương ứng với cạnh BC I là tâm đường tròn nội tiếp #5. Lời kết Vâng, như vậy là qua bài viết này thì bạn đã biết hoặc nhớ lại tính chất và định nghĩa của đường trung tuyến, đường cao, đường trung trực, đường phân giác trong một tam giác rồi đúng không. Trong một tam giác đều thì trọng tâm, trực tâm, tâm đường tròn ngoại tiếp, tâm đường tròn nội tiếp sẽ trùng nhau. Trong một tam giác bất kỳ thì trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác luôn nằm trên một đường thẳng, hay nói cách khác là thẳng hàng nhau. Đó là đôi lời mở rộng kiến thức mà mình muốn gửi đến các bạn. Hi vọng bài viết này sẽ hữu ích với bạn, chúc các bạn học tập tốt, xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ! Đọc thêm: CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Bài viết đạt: 5/5 sao - (Có 1 lượt đánh giá) Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé ! Adblock test (Why?)

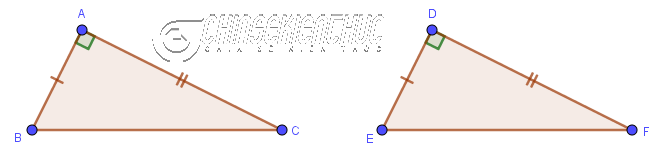
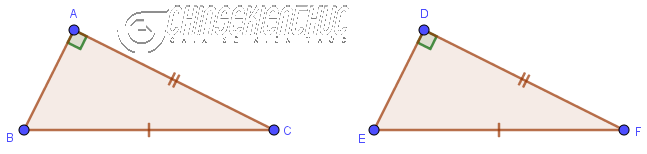
4 cách chứng minh hai tam giác vuông bằng nhau (có ví dụ) Posted: 04 Apr 2022 03:01 AM PDT Ở bài viết này chúng ta sẽ cùng nhau tìm hiểu về bốn trường hợp bằng nhau trong hai tam giác vuông. Tất nhiên bạn có thể vận dụng kiến thức cũ trong bài viết (3 cách chứng minh hai tam giác bằng nhau) để chứng minh hai tam giác vuông bằng nhau. Tuy nhiên, đó không phải là phương án tối ưu nhất, tam giác vuông là tam giác đặc biệt nên sẽ có các cách đặc biệt để chứng minh. Việc vận dụng tốt 4 cách chứng minh 2 tam giác vuông bằng nhau này sẽ là phương pháp hoàn hảo nhất, giúp bạn tiết kiệm được khá nhiều công sức và thời gian khi làm bài tập. Mục Lục Nội Dung Trường hợp #1. Hai cạnh góc vuông bằng nhau Nếu 2 cạnh góc vuông của tam giác vuông này lần lượt bằng 2 cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đã cho bằng nhau. 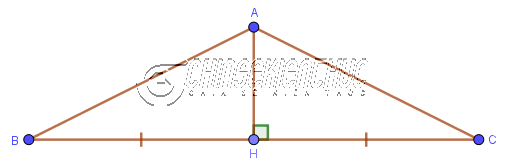$\left.\begin{array}{} AB=DE \\ AC=DF\end{array}\right\} \Rightarrow \triangle ABC = \triangle DEF$ Dễ thấy trường hợp này tương ứng với trường hợp Cạnh Góc Cạnh Ví dụ 1: Cho tam giác ABC có AH là đường cao và H là trung điểm của cạnh BC. 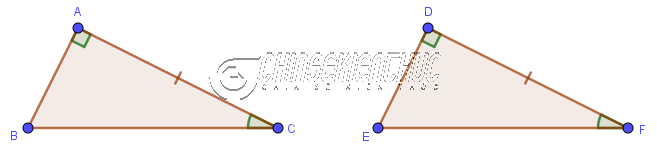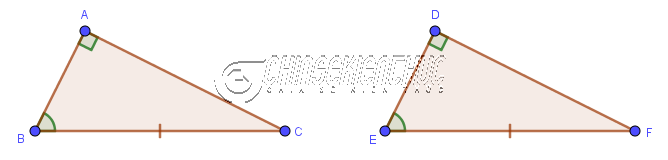Chứng minh tam giác ABH bằng tam giác ACH Xét tam giác ABH và tam giác ACH $\widehat{AHB}=\widehat{AHC}=90^o$ AH là cạnh chung của hai tam giác BH=CH (H là trung điểm của cạnh BC) => Vậy tam giác ABH bằng tam giác ACH Trường hợp #2. Một cạnh góc vuông và một góc nhọn bằng nhau Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này lần lượt bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đã cho bằng nhau. 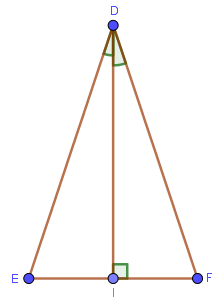$\left.\begin{array}{} AC=DF \\ \hat{C}=\hat{F} \end{array}\right\} \Rightarrow \triangle ABC = \triangle DEF$ Trường hợp này tương ứng với trường hợp Góc Cạnh Góc Ví dụ 2: Cho tam giác DEF có DI là đường cao cũng là đường phân giác. Chứng minh tam giác DEI bằng tam giác DFI. 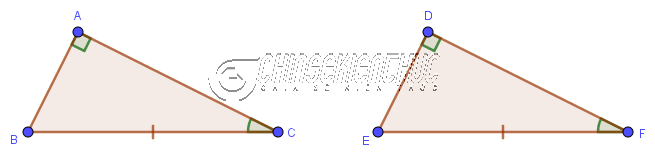Xét tam giác DEI và tam giác DFI $\widehat{DIE}=\widehat{DIF}=90^o$ DI là cạnh chung của hai tam giác $\widehat{EDI}=\widehat{FDI}$ (DI là tia phân giác của $\widehat{EDF}$) => Vậy tam giác DEI bằng tam giác DFI Trường hợp #3. Cạnh huyền và một góc nhọn bằng nhau Nếu cạnh huyền và một góc nhọn của tam giác vuông này lần lượt bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác đã cho bằng nhau. 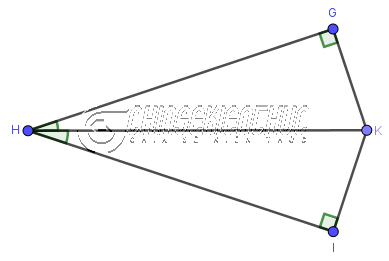$\left.\begin{array}{} BC=EF \\ \hat{B}=\hat{E} \end{array}\right\} \Rightarrow \triangle ABC = \triangle DEF$ Hoặc: $\left.\begin{array}{} BC=EF \\ \hat{C}=\hat{F} \end{array}\right\} \Rightarrow \triangle ABC = \triangle DEF$ Thật vậy … Tổng ba góc trong một tam giác luôn bằng 180 độ Hai góc của hai tam giác tương ứng bằng nhau => Suy ra góc còn lại cũng bằng nhau Vậy trường hợp này tương ứng với trường hợp Góc Cạnh Góc Ví dụ 3: Cho tứ giác GHIK có $\hat{G}=\hat{I}=90^o$ và HK là tia phân giác của $\hat{H}$. Chứng minh tam giác GHK bằng với tam giác IHK. 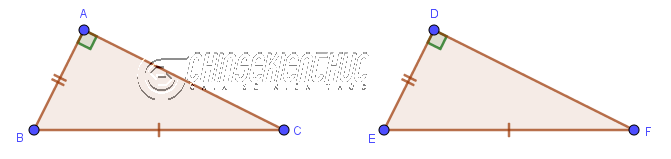Xét tam giác vuông GHK và tam giác vuông IHK HK là cạnh chung $\widehat{GHK}=\widehat{IHK}$ (HK là tia phân giác của $\hat{H}$ ) => Vậy tam giác GHK bằng tam giác IHK Trường hợp #4. Cạnh huyền và một cạnh góc vuông bằng nhau Nếu cạnh huyền và cạnh góc vuông của tam giác vuông này lần lượt bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác đã cho bằng nhau. $\left.\begin{array}{} BC=EF \\ AB=DE \end{array}\right\} \Rightarrow \triangle ABC = \triangle DEF$ Hoặc: $\left.\begin{array}{} BC=EF \\ AC=DF \end{array}\right\} \Rightarrow \triangle ABC = \triangle DEF$ Thật vậy … Trong một tam giác vuông luôn có bình phương độ dài của cạnh huyền bằng tổng bình phương độ dài của hai cạnh góc vuông Hai tam giác vuông đã cho có một cạnh huyền và một cạnh góc vuông bằng nhau Suy ra cạnh góc vuông còn lại chắc chắn cũng bằng nhau => Vậy trường hợp này tương ứng với trường hợp Cạnh Cạnh Cạnh Lời kết Đến đây chúng ta đã cùng nhau tìm hiểu xong 4 cách để chứng minh 2 tam giác vuông bằng nhau một cách khá chi tiết và đầy đủ rồi. Chúng ta cũng đã áp dụng định lý tổng ba góc trong một tam giác và định lý Pytago để chứng minh cho Trường hợp 3 và Trường hợp 4. Riêng Trường hợp 4 thì bạn có thể xem nó là một hệ quả của định lý Pytago. Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ! CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Bài viết đạt: 5/5 sao - (Có 1 lượt đánh giá) Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé ! Adblock test (Why?)

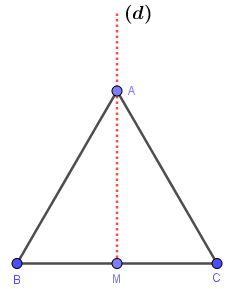
Cách vẽ tam giác đều, tứ giác đều, ngũ giác đều và lục giác đều Posted: 04 Apr 2022 02:57 AM PDT Hôm nay chúng ta sẽ cùng nhau tìm hiểu cách vẽ các đa giác đều thường gặp, như là tam giác đều, tứ giác đều, ngũ giác đều và lục giác đều. Tương ứng với mỗi một đa giác đều thì mình sẽ hướng dẫn một hoặc một vài cách vẽ, cũng như  cách dựng khác nhau. Mỗi cách vẽ/ cách dựng sẽ sử dụng các công cụ khác nhau, vì vậy bạn cần chuẩn bị đầy đủ thước thẳng, compa và thước đo góc nếu muốn thực hành tất cả các cách trong bài hướng dẫn này nhé. Mục Lục Nội Dung #1. Cách vẽ tam giác đều Phương pháp 1. Chỉ sử dụng thước thẳng Bước 1. 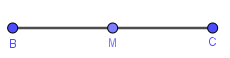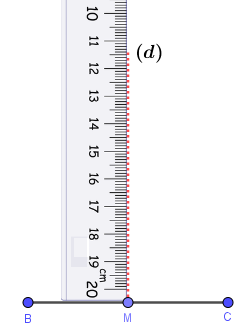Vẽ đoạn thẳng BC Bước 2. Vẽ đường trung trực của đoạn thẳng BC Bước 2.1. 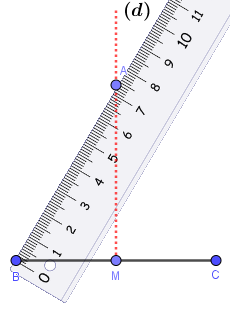Vẽ trung điểm M Bước 2.2. Vẽ đường thẳng (d) đi qua M và vuông góc BC Bước 3. Vẽ điểm A trên (d) sao cho BA = BC Bước 4. 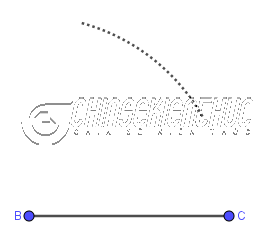Vẽ đoạn thẳng BA, CA Phương pháp 2. Sử dụng thước thẳng và compa Bước 1. 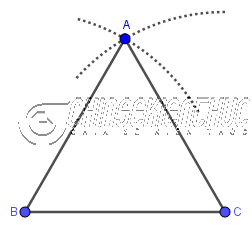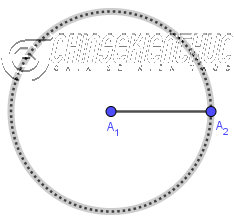Vẽ cạnh BC Bước 2. 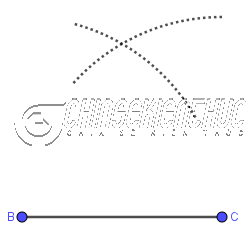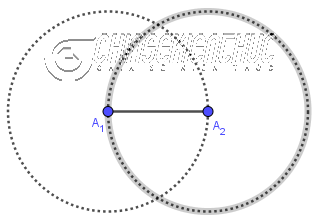Vẽ đường tròn/ cung tròn tâm B bán kính BC Bước 3. 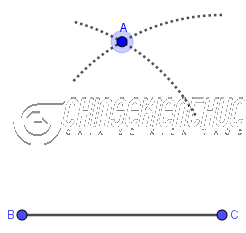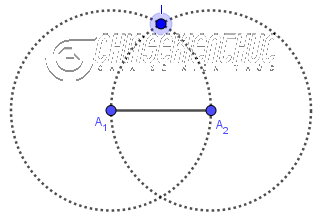Vẽ đường tròn/ cung tròn tâm C bán kính CB Bước 4. 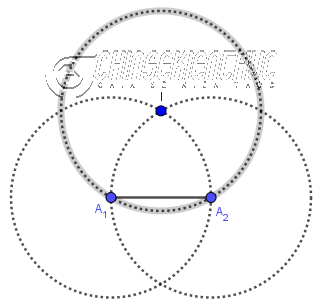Vẽ giao điểm A của hai đường tròn/ cung tròn Bước 5. 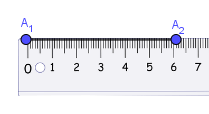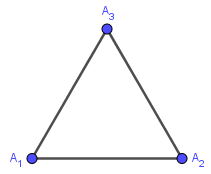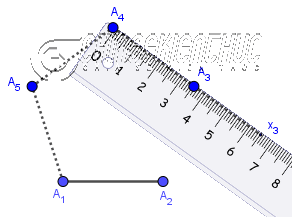Vẽ các đoạn thẳng BA, CA Phương pháp 3. Sử dụng thước thẳng và thước đo góc Bước 1. 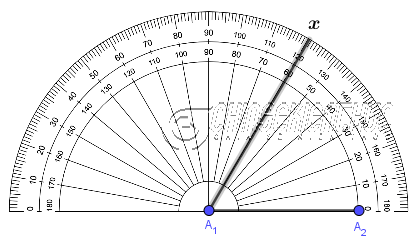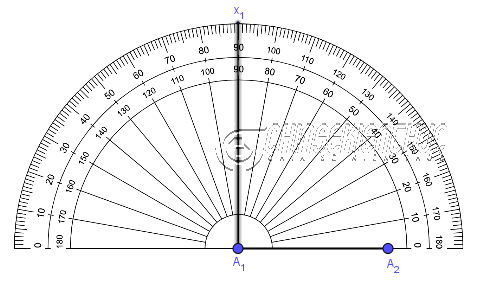Vẽ đoạn thẳng $A_1A_2$ Bước 2. 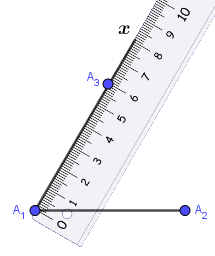Vẽ $\widehat{A_2A_1x}=60^o$ Bước 3. Trên tia $A_1x$ vẽ điểm $A_3$ sao cho $A_1A_3=A_1A_2$ Bước 4. 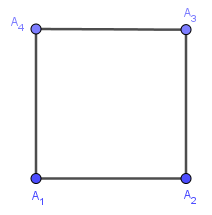Vẽ các đoạn thẳng $A_2A_3, A_3A_1$ #2. Cách vẽ tứ giác đều và hình vuông Phương pháp 1. Sử dụng thước thẳng và compa Phương pháp này khá phức tạp, không có nhiều ứng dụng trong thực tiễn, vì vậy mình không hướng dẫn. Phương pháp 2. Sử dụng thước thẳng và thước đo góc Bước 1. 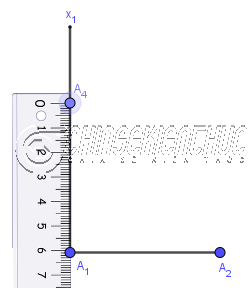Vẽ đoạn thẳng $A_1A_2$ Bước 2. Vẽ $\widehat{A_2A_1x_1}=90^o$ Bước 3. 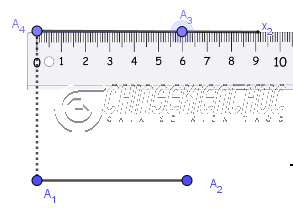Trên tia $A_1x_1$ vẽ điểm $A_4$ sao cho $A_1A_4=A_1A_2$ Bước 4. Thực hiện tương tự Bước 2 và Bước 3 để vẽ điểm $A_3$ Bước 5. 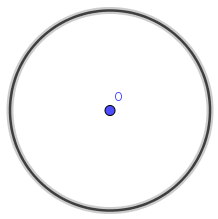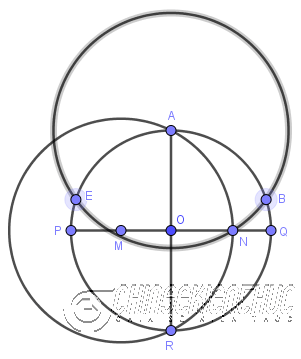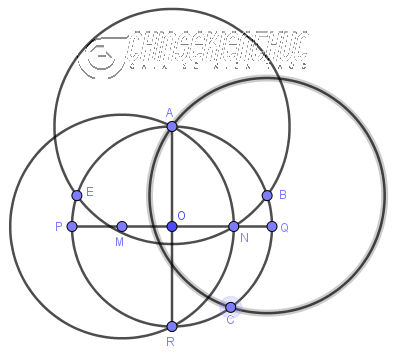Vẽ các đoạn thẳng $A_2A_3, A_3A_4, A_4A_1$ #3. Cách vẽ ngũ giác đều Phương pháp 1. Sử dụng thước thẳng và compa Bước 1. 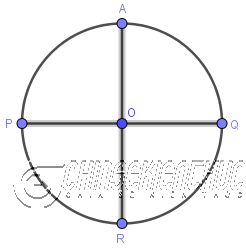Vẽ đường tròn tâm O Bước 2. 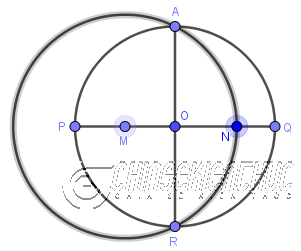Vẽ đường kính AR và PQ (AR vuông góc PQ tại O) Bước 3 … Vẽ M là trung điểm PO Vẽ đường tròn tâm M bán kính MA, đường tròn này cắt OQ tại N Bước 4. Vẽ đường tròn tâm A bán kính AN, đường tròn này cắt đường tròn tâm O tại E, B Bước 5. Vẽ đường tròn tâm B bán kính BA, đường tròn này cắt đường tròn O tại C Bước 6. Vẽ đường tròn tâm E bán kính EA, đường tròn này cắt đường tròn O tại D Bước 7. Vẽ các đoạn thẳng AB, BC, CD, DE, EA Phương pháp 2. 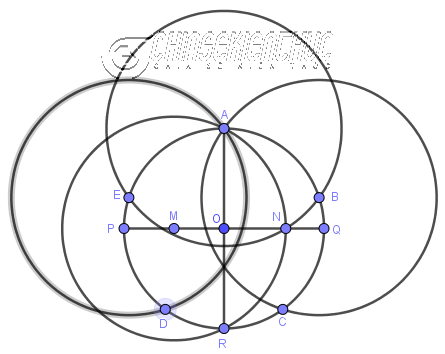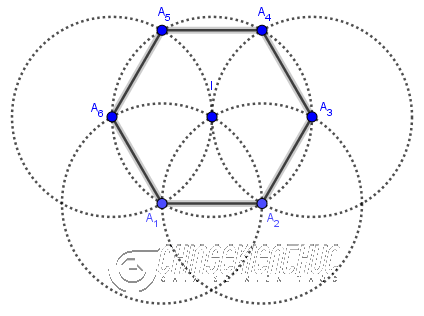Sử dụng thước thẳng và thước đo góc Thực hiện tương tự các bước vẽ tứ giác đều với $\widehat{A_2A_1A_5}=108^o$ #4. Cách vẽ lục giác đều Phương pháp 1. Vẽ bằng thước thẳng và compa Bước 1. Vẽ đoạn thẳng $A_1A_2$ Bước 2. Vẽ đường tròn tâm $A_1$ bán kính $A_1A_2$ Bước 3. Vẽ đường tròn tâm $A_2$ bán kính $A_2A_1$ Bước 4. Vẽ giao điểm I của hai đường tròn ở Bước 2 và Bước 3 Bước 5. 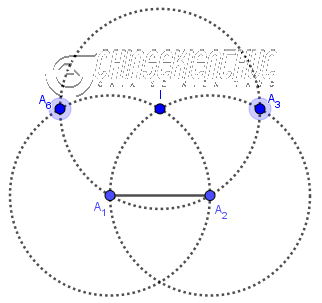Vẽ đường tròn tâm I bán kính $IA_1$ Bước 6. 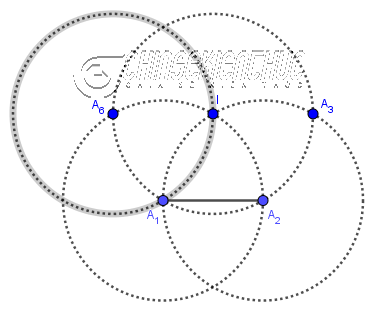Vẽ giao điểm $A_6$ và $A_3$ của đường tròn tâm I với hai đường tròn Bước 2 và Bước 3 Bước 7. 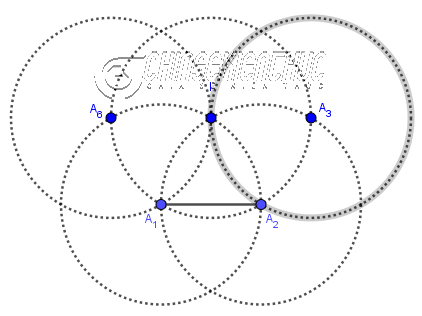Vẽ đường tròn tâm $A_6$ bán kính $A_6 I$ Bước 8. 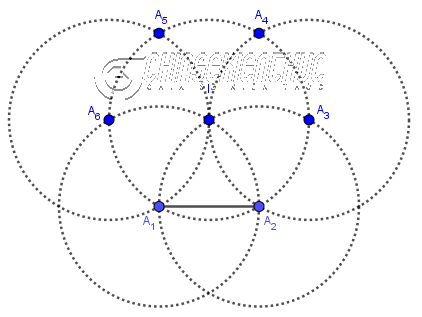Vẽ đường tròn tâm $A_3$ bán kính $A_3 I$ Bước 9. Vẽ giao điểm $A_5, A_4$ của hai đường tròn ở Bước 7, Bước 8 và đường tròn tâm I Bước 10. 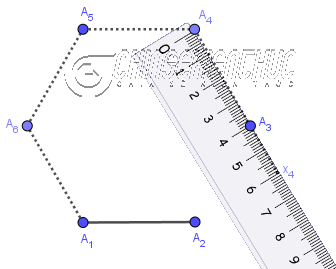Vẽ các đoạn thẳng $A_2A_3, A_3A_4, A_4A_5, A_5A_6, A_6A_1$ Phương pháp 2. Vẽ bằng thước thẳng và thước đo góc Thực hiện tương tự các bước vẽ tứ giác đều với $\widehat{A_2A_1A_6}=180^o$ #5. Lời kết Vâng, như vậy là mình đã hướng dẫn xong cho bạn cách vẽ tam giác đều, tứ giác đều, ngũ giác đều và lục giác đều bằng rất nhiều cách rồi ha. Chúng ta nên phân biệt cụm từ vẽ hình và dựng hình hay công cụ được sử dụng khi vẽ hình và công cụ được sử dụng khi dựng hình. Vẽ hình có thể sử dụng thước thẳng, thước độ góc, compa, … Dựng hình chỉ có thể sử dụng thước thẳng và compa Nếu là vẽ hình thì có thể vẽ được tất cả các đa giác đều. Còn nếu là dựng hình thì không thể dựng được tất cả, dễ thấy nhất là thất giác đều. Tuy nhiên, đa giác đều nào dựng được thì chắc chắn là rất chính xác, có thể chứng minh cách dựng là bằng Toán học. Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ! Đọc thêm: CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Bài viết đạt: 5/5 sao - (Có 1 lượt đánh giá) Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé ! Adblock test (Why?)

You are subscribed to email updates from Blog chia sẻ kiến thức: Máy tính - Công nghệ & Cuộc Sống. To stop receiving these emails, you may unsubscribe now.	Email delivery powered by Google
Google, 1600 Amphitheatre Parkway, Mountain View, CA 94043, United States